Calibration of Fluorescent Calcium Indicators
Adapted from Imaging: A Laboratory Manual (ed. Yuste). CSHL Press, Cold Spring Harbor, NY, USA, 2010.INTRODUCTION
During the past decades, many different fluorescent indicators have been developed for measuring intracellular ion concentrations. Of particular interest are fluorescent calcium indicators because of the fundamental role of Ca2+ in various cellular processes such as contraction, secretion, and gene activation. For a quantitative understanding of the physiological roles of Ca2+, fluorescence signals measured with calcium indicators have to be converted to intracellular free calcium concentration ([Ca2+]i). Similarly, changes in [Ca2+]i and the underlying calcium fluxes need to be inferred from the corresponding fluorescence changes. This article describes the theoretical background and the various principal methods for the calibration of calcium imaging data.
BACKGROUND
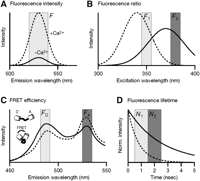
Fluorescent calcium indicators are universal tools for studying intracellular signaling and therefore are used in all fields of cell biology. In neurobiology, they have been applied to study many functional aspects, for example, the role of Ca2+ in neurotransmitter release and in postsynaptic signal integration. For each specific application, the most suitable indicator dye can be chosen from a large palette of indicators, which differ with respect to their affinity, mobility, solubility, and fluorescence properties. Two large groups of indicators exist: (1) synthetic organic molecules (mostly derived from the fast calcium buffer BAPTA; Tsien 1980), which can be loaded into cells and subcellular compartments using various techniques (Tsien 1989; Göbel and Helmchen 2007); and (2) genetically encoded calcium indicators based on fluorescent proteins (for reviews, see Miyawaki 2003; Hires et al. 2008; Mank and Griesbeck 2008) (see Miyawaki et al. 2010; Tian et al. 2011). Common to all indicators is that their fluorescence is sensitive to [Ca2+]i in at least one respect; Ca2+ binding may cause changes in fluorescence intensity, spectral shifts, or changes in fluorescence resonance energy transfer (FRET) efficiency (Fig. 1). In addition, the fluorescence lifetime may change upon Ca2+ binding. In the following, the theoretical background and the basic principles of converting fluorescence signals to [Ca2+]i changes are described. Note that equivalent considerations apply to measurements using fluorescent indicators of other ion species (e.g., H+, Na+, Cl–).
Changes in fluorescence properties of calcium indicators used for calibration. (A) Changes in the fluorescence intensity result from changes of the quantum yield and the absorption of a dye upon Ca2+ binding. An emission spectrum similar to that of Calcium Green-1 is schematically shown with higher intensities of the Ca2+ bound form (dashed line) compared to the unbound form (solid line). Other indicators (e.g., Fura-Red [not shown]) show decreases in the intensity. In single-wavelength measurements, the dye is excited at a single wavelength, and the emission intensity F is collected in a spectral window around the peak of the emission spectrum. (B) Spectral shifts allow ratiometric measurements because the ratio of the fluorescence intensities F1 and F2 measured at two different wavelengths in this case is sensitive to Ca2+ binding. The drawing schematically shows an excitation spectrum similar to that of Fura-2 at zero Ca2+ concentration (solid line) and at saturating Ca2+ levels (dashed line). The peak of the spectrum shifts to shorter wavelength upon Ca2+ binding. Note that excitation at 360 nm results in [Ca2+]i-insensitive fluorescence emission, defining the so-called isosbestic wavelength. (C) Changes in fluorescence resonance energy transfer (FRET) efficiency are used in the case of tandem GFP-based indicators, which use a donor (D) fluorescent protein linked via a Ca2+-sensitive spacer to an acceptor (A) fluorescent protein. The emission spectrum of a yellow cameleon (with enhanced cyan fluorescent protein [ECFP] and enhanced yellow fluorescent protein [EYFP] as donor and acceptor, respectively) is shown schematically at low (solid line) and high (dashed line) [Ca2+]i level (excitation ∼430 nm). The distance between the two fluorescent proteins decreases upon Ca2+ binding, which, as a result of enhanced FRET efficiency, causes the donor emission (FD) to decrease and the acceptor fluorescence (FA) to increase, thus permitting ratiometric measurements. (D) Alternatively, changes in the fluorescence lifetime have been used for calibration. Fluo-3, for example, shows a shorter fluorescence lifetime in the Ca2+ bound form (dashed line) compared to the unbound form (solid line) as illustrated schematically. Other indicators show an increase of fluorescence lifetime upon Ca2+ binding. As a result, the ratio of the number of photons N1 and N2 that are detected in two time windows during the fluorescence decay is sensitive to [Ca2+]i. Not all indicators necessarily are [Ca2+]i sensitive with respect to all the properties shown in A–D.
Changes in Fluorescence Intensity
The emission intensity F arising from an observation volume V (e.g., a single cell or a cell compartment loaded with a fluorescent dye) depends on the number of dye molecules, the illumination
intensity I0, the dye absorption α, the quantum yield of the dye QF, the photon-collection efficiency Φ of the optical setup, and the quantum efficiency (QE) of the detector QD: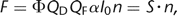
1where n is the molar amount of dye molecules in V. Here, all factors that depend on dye properties or the experimental setup have been “lumped” together in a single proportionality
constant S. In the case of calcium indicators, we have to consider separately the molar amounts nf and nb of the free and the Ca2+-bound indicator forms, respectively. They differ with respect to their quantum yield and their absorption and therefore contribute
to F with different factors Sf and Sb, respectively:
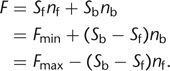2
The equation has been rewritten using the definitions for the fluorescence at zero Ca2+ concentration Fmin = Sfntot and at saturating [Ca2+]i levels, Fmax = Sbntot, with ntot = nf + nb, and assuming a fluorescence increase upon Ca2+ binding. The indicator fluorescence thus depends on the relative amounts of the free and bound forms. Assuming 1:1 complexation
of Ca2+ with the dye, nf and nb vary according to the law of mass action: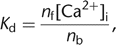
3where Kd is the dissociation constant of the indicator. Equations 1–3 are the basis for all conversion equations that relate fluorescence signals to [Ca2+]i values. Before introducing these equations, however, we first have to clarify some important issues concerning the dye concentration
and the subtraction of background fluorescence.
Dye Concentration and Background Subtraction
A central assumption underlying Equation 1 is that all dye molecules sense the same illumination intensity, meaning that no inner filtering occurs. In general, the
intensity of light that is absorbed by a fluorescent layer of thickness l is given by the Beer-Lambert law,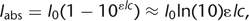
4where ϵ is the molar extinction coefficient and c is the dye concentration. The approximation of a linear relationship between Iabs and c as used in Equation 1 is only valid if c << [ln(10)ϵl]–1. This sets an upper limit to the useful dye concentration range. Extinction coefficients of calcium indicators typically
are in the range of 20,000–100,000 m–1 cm–1 (Molecular Probes Handbook, Invitrogen). Thus, for measurements on small cells with 10-µm diameter, the indicator concentration
should be well below 5–20 mm. In thick cuvettes of ∼1 cm path length, which are sometimes used for in vitro calibration, much smaller concentrations have
to be used (typically 1 µm). At very high concentration, dye fluorescence in addition may be reduced because of self-quenching. Furthermore, for measurements
of intracellular calcium dynamics, the choice of indicator concentration is constrained by the Ca2+-buffering effect exerted by the indicator itself. Depending on the endogenous Ca2+-buffering capacity, even a relatively low concentration of a high-affinity indicator (100 µm) may reduce and prolong [Ca2+]i changes several-fold (Neher 1995; Neher 2010; Helmchen and Tank 2011). Low-affinity dyes can circumvent this problem, partly because they can be applied in relatively high concentration without
altering [Ca2+]i dynamics significantly. The resulting fluorescence signals, however, may be very small (see below).
Optical components, the bathing solution, and endogenous fluorophores all add background to the indicator fluorescence given in Equation 2. Because background fluorescence increases the noise level, it should be minimized (Moore et al. 1990). Importantly, any background fluorescence Fbkg must be subtracted from the observed fluorescence (F = Fobs – Fbkg) before applying equations for conversion to [Ca2+]i. This supposedly simple step in practice often is not so easy. In imaging experiments on brain slices, a relatively large background arises from endogenous fluorophores of the surrounding tissue, especially with ultraviolet (UV) excitation. Also, the background may change during an experiment because of bleaching (Eilers et al. 1995). Therefore, it is necessary to perform background measurements throughout the experiment in a slice region nearby the cell of interest, for example, directly before and after each recording episode (Helmchen et al. 1996). A more severe problem occurs when tissue is bulk-loaded with AM-esters of calcium indicators leading to rather diffuse staining (Stosiek et al. 2003). In this case, the best possible region for background estimation is a relatively dye-free region near the cell (e.g., a blood vessel lumen) because the stained neuropile immediately next to the cell would provide a poor background estimate as it contains numerous stained and [Ca2+]i-sensitive axons and dendrites. A more rigorous and sophisticated approach is to estimate the background fluorescence level within a particular region of interest based on the temporal dynamics of the individual pixels within this region (Chen et al. 2006).
CALIBRATION METHODS
Single-Wavelength Measurements
One class of calcium indicators responds to Ca2+-binding with an up- or downscaling of the fluorescence intensity without showing appreciable spectral shifts (Fig. 1A). Almost all synthetic indicators excited in the visible-wavelength range belong to this group. As a result, all available information on Ca2+ concentration is obtained from dye excitation at a single wavelength.
In principle, the fluorescence signal F measured at a single excitation wavelength can be converted to [Ca2+]i by assuming equilibrium between Ca2+ and the indicator and combining Equations 2 and 3: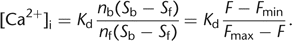
5
Although this equation is readily applicable to bulk measurements of cuvette solutions (e.g., of cell suspensions), it is
impractical for imaging experiments because Fmin and Fmax would need to be determined independently for each observation volume (i.e., each pixel), which is impossible. If, however,
ratios of intensities are used instead of absolute intensities, all spatial variations in cell thickness, total dye concentration,
and detection efficiency or illumination intensity cancel out and thus are normalized (see Equation 1). For time-dependent measurements, normalization by rationing most easily is achieved by expressing the signal as relative
fluorescence change: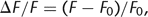
6where F0 denotes the background-subtracted pre-stimulus fluorescence level. For ΔF/F (“ΔF over F”), the following conversion equation can be derived (Lev-Ram et al. 1992):
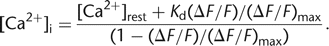7
Here, [Ca2+]rest is the resting calcium concentration and (ΔF/F)max is the maximal change upon dye saturation, which, for example, can be estimated using very strong stimulation or cell destruction at the end of an experiment. The major drawback of this and other related single-wavelength equations (Vranesic and Knöpfel 1991; Neher and Augustine 1992; Wang et al. 1995) is that an a priori knowledge of [Ca2+]rest is required, which in principle needs to be obtained independently, for example, using an initial ratiometric measurement (see below). Note also that (ΔF/F)max depends on [Ca2+]rest, which therefore is presumed constant throughout the experiment. Despite these difficulties, a reasonable value of [Ca2+]rest may be assumed (50–100 nm) under certain conditions, in particular, when the health of the cell is monitored in parallel by additional methods like electrophysiology.
An alternative single-wavelength approach that circumvents the necessity for an independent measurement of [Ca2+]rest is based on rearranging Equation 5 differently (Maraval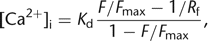l et al. 2000):
8where Rf denotes the dynamic range Fmax/Fmin of the indicator. The idea is that the ratio of the actual fluorescence to the saturating fluorescence F/Fmax reflects the [Ca2+]i level, given that the Kd and Rf are known. Rf thus needs to be determined initially for an indicator (e.g., using an in vitro calibration procedure), and it turns out
that for large Rf values, the conversion to [Ca2+]i is relatively robust against uncertainties in its exact value. The remaining calibration procedure is then to estimate the
saturating fluorescence level Fmax (or the related (ΔF/F)max, respectively) intermittently during the experiment and/or at its end, which for high-affinity indicators can be achieved
by inducing trains of high-frequency action potentials (Maravall et al. 2000).
If only small fluorescence changes are evoked and if the indicator is far from saturation (e.g., in the case of low-affinity
calcium indicators), the single-wavelength equations can be linearized to provide an estimate of the change in [Ca2+]i: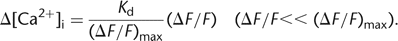
9
For low-affinity indicators, however, it may be difficult to induce large enough calcium influx to determine the saturating fluorescence changes.
Dual-Wavelength Ratiometric Measurements
A second group of indicators undergoes shifts in the excitation or emission spectrum upon Ca2+ binding (Fig. 1B). These spectral shifts can be exploited for [Ca2+]i calibration because, in this case, the ratio R = F1/F2 of the intensities measured at two wavelengths depends on [Ca2+]i. The ratiometric method is the most often applied calibration method because R is independent of dye concentration, optical
path length, and illumination intensity. The intensities F1 and F2 are given according to Equation 2: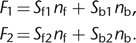
10
Note that for actual measurements, both intensities have to be corrected for background fluorescence at the corresponding
excitation or emission wavelengths before taking the ratio. From Equations 3 and 10, the standard equation for ratiometric measurements can be derived (Grynkiewicz et al. 1985):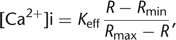
11with the ratios at zero Ca2+ concentration Rmin = (Sf1/Sf2), at saturating Ca2+ concentrations Rmax = (Sb1/Sb2), and an effective binding constant Keff = Kd(Sf2/Sb2).
The design and use of ratio imaging systems have been described in several reviews (see, e.g., Neher 1989; Tsien and Harootunian 1990). Dual-wavelength measurements with high time resolution require rapid switching of wavelengths. Alternatively, Equation 11 can be used to obtain an initial value of [Ca2+]rest for subsequent single-wavelength measurement and application of Equation 7. For a more detailed description of how to use Fura-2, the most popular ratiometric dye, see Neher (2010). The ratiometric method also has been extended to mixtures of non-ratiometric dyes that result in Ca2+-sensitive fluorescence ratios (Lipp and Niggli 1993; Oheim et al. 1998).
Changes in FRET Efficiency
Genetically encoded calcium indicators consist either of a single modified green fluorescent protein (GFP) exhibiting Ca2+-sensitive fluorescence (Baird et al. 1999; Nakai et al. 2001), or they are based on changes in FRET between two spectral variants of fluorescent proteins. For example, cameleons are fusion proteins of two fluorescent proteins linked via a spacer consisting of calmodulin and the calmodulin-binding peptide M13 (Miyawaki et al. 1997). Ca2+ binding to calmodulin causes a conformational change, which brings the two fluorescent proteins closer together and thereby causes an increase in the FRET efficiency. This change can be read out by measuring the change in the ratio of the donor and acceptor emission intensities in two appropriate spectral windows (Fig. 1C). Because the emission spectra of donor and acceptor typically have some overlap, cross talk may have to be taken into account (Gordon et al. 1998). As genetically encoded calcium indicators often display cooperativity of multiple Ca2+-binding sites, conversion equations incorporating a Hill coefficient >1 may need to be applied (Palmer et al. 2006). For further information on genetically encoded calcium indicators, see Miyawaki et al. (2010).
Changes in Fluorescence Lifetime
As an alternative to the intensity, the fluorescence lifetime can be used as an indicator of Ca2+ binding (Lakowicz et al. 1992; Draaijer et al. 1995). After the end of excitation, the fall-off in fluorescence intensity reflects the lifetime of the excited state of the dye molecules (Fig. 1D). In the simplest case, the decay is described by a single exponential curve with a fluorescence lifetime constant τL, which typically is in the nanosecond range; in general, multiple decay components are present. Several calcium indicators show useful Ca2+-dependent fluorescence lifetime changes (Draaijer et al. 1995; Wilms and Eilers 2007).
One method to measure the fluorescence lifetime is time-gated photon detection following a brief exciting laser pulse. The
ratio of the numbers of photons N1 and N2 that are detected in two time windows following the excitation pulse provides an effective fluorescence lifetime τeff = Δt/log(N1/N2), where Δt is the width of the windows (Fig. 1D). τeff can also be obtained from the phase shift and the change in amplitude when a modulated light source is used (Lakowicz et al. 1992). Both the free and the Ca2+-bound forms of the indicator contribute to the effective fluorescence lifetime, which relates to [Ca2+]i via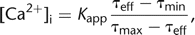
12where τmin and τmax denote the lifetimes of the bound and free indicator forms, respectively, assuming a lifetime decrease, and Kapp denotes an apparent dissociation constant. Quantification of [Ca2+]i from lifetime measurements can be further improved by using time-correlated single-photon counting with a pulsed laser source
and multi-exponential fitting routines (Wilms et al. 2006).
Because lifetimes are independent of dye concentration and illumination intensity, a calibration according to Equation 12 is readily applied to imaging experiments. Kapp depends on the relative intensities of the free and bound indicator forms. Interestingly, the apparent affinity of an indicator showing a spectral shift therefore can be tuned in a wide range simply by selecting the excitation wavelength (Szmacinski and Lakowicz 1995). A fast fluorescence lifetime imaging (FLIM) microscope enabling [Ca2+]i measurements with frame rates of >50 Hz has been presented in Agronskaia et al. (2003). Lifetime-based Ca2+ imaging is also relatively straightforward to add on to microscopic techniques that inherently use pulsed laser sources for excitation, such as two-photon laser scanning microscopy (Wilms et al. 2006; Kuchibhotla et al. 2009). Finally, fluorescence lifetime measurements of the combined donor/acceptor emission can be used as an alternative means to determine changes in FRET efficiency (Harpur et al. 2001).
Total Calcium Flux Measurements
Calcium indicators are mainly used for measuring [Ca2+]i. However, as calcium chelators they inevitably and sometimes significantly alter the magnitude and the time course of [Ca2+]i changes (see Neher 2010; Helmchen and Tank 2011). This problem of indicator buffering is separate from the problem of an accurate calibration: Even if the concentration
values calculated are correct, they may not reflect the physiological [Ca2+]i levels reached in the absence of the indicator. On the other hand, buffering by the indicator can be exploited to measure
Ca2+ fluxes (Schneggenburger et al. 1993; Neher 1995). When loaded in excess into a cell compartment, the indicator molecules outcompete the endogenous Ca2+ buffers and capture virtually all ions that enter the cytosol. Under such an “overload condition,” the change in absolute
fluorescence intensity is proportional to the total calcium charge QCa injected: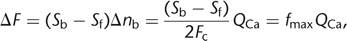
13where Fc is Faraday’s constant. This overload method has been used to determine fractional Ca2+ currents through ligand-gated ion channels (Schneggenburger et al. 1993; Neher 1995; Bollmann et al. 1998) and the total calcium influx during an action potential (Helmchen et al. 1997; Bollmann et al. 1998).
DISCUSSION
In summary, many different fluorescent calcium indicators are available, and different methods exist for quantifying various Ca2+-signaling aspects from the observed fluorescence signals. For quantitative measurements, a careful understanding of the indicator properties under the experimental conditions and of potential interferences of other binding partners (e.g., H+, Mg++) is required. As shown in the examples in Figure 2, employment of different types of indicators at appropriate concentration can be highly informative. Single-wavelength measurements are well suited to measure fast signals as they provide the highest possible temporal resolution. Combined with initial ratiometric measurements or following careful determination of the dissociation constant and the dynamic range of the indicator, they can also be used for calibrated [Ca2+]i measurements.
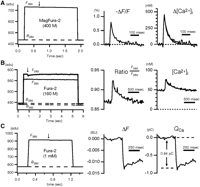
Calibration examples from measurements of single action potential-induced fluorescence changes in calyx-type presynaptic terminals in the medial nucleus of the trapezoid body (MNTB). The fluorescence (F) averaged over the entire terminal was measured using a fast charge-coupled device (CCD) camera (expressed in analog-to-digital units [adu]). Background fluorescence (B) from a nearby region was determined immediately before and after each measurement (interpolated by dashed lines). Timing of single action potentials is indicated by arrows. The temperature was 35°C. (A) Single-wavelength measurement using the low-affinity indicator MagFura-2. A single action potential caused a small ΔF/F change of <1%, which was converted to Δ[Ca2+]i using Equation 9. Average of 50 traces. (B) Ratiometric measurement using Fura-2. The ratio between the fluorescence intensities at the isosbestic wavelength (F360) and at 380 nm (F380) was evaluated and converted to [Ca2+]i using Equation 11. Note that an estimate of [Ca2+]rest is obtained, but that the [Ca2+]i transient is profoundly reduced in amplitude and prolonged owing to the added Fura-2 Ca2+-buffering capacity. No averaging. (C) Calcium flux measurement using Fura-2 overload. At high Fura-2 concentration, a single action potential induces only a small fluorescence decrement ΔF380 of ∼5 adu (≈1% ΔF/F), which is expressed in bead units (BU) and then converted to the total calcium charge QCa using Equation 13. Average of 20 traces. For further details, see Calibration Protocols for Fluorescent Calcium Indicators (Helmchen 2011).
A general problem of calcium measurements using imaging systems is that they represent [Ca2+]i levels averaged over sizable cytosolic volumes, in the best case, over the diffraction-limited focal volume. They are therefore blind to highly localized [Ca2+]i gradients and may underestimate the actual [Ca2+]i level reached at the site of action, for example, the binding to a Ca2+ sensor. Two approaches may overcome this problem: (1) Ca2+ uncaging by flash photolysis (see Zayat et al. 2010), causing spatially homogeneous [Ca2+]i elevations, which can be quantified using the methods described here; and (2) the application of indicator forms that are targeted to the intracellular sites of interest (e.g., by genetic means).
- © 2011 Cold Spring Harbor Laboratory Press
