Getting Started in Stereology
Adapted from Basic Stereology for Biologists and Neuroscientists by Mark J. West. CSHL Press, Cold Spring Harbor, NY, USA, 2012.Abstract
Stereology involves sampling structural features in sections of tissue with geometrical probes. This article discusses some practical issues that must be dealt with when getting started in stereology, including tissue preparation methods and determining how many tissue sections and probes are needed to make a stereological estimate.
INTRODUCTION
Stereology provides meaningful quantitative descriptions of the geometry of three-dimensional (3D) structures from measurements that are made on two-dimensional (2D) images. (See Introduction to Stereology [West 2012a].) One of the most common questions asked by those starting out in stereology is how many sections and probes are needed to make a stereological estimate. There is no set a priori answer to this question. To determine how many sections should be used in a stereological analysis and the numbers and sizes of the probes that should be applied to these sections, it is necessary to know something regarding the variability of the feature of interest in the individuals in both control and experimental groups. This includes information regarding the spatial distribution of the feature of interest in a typical individual and a feeling for the group mean differences that can be considered biologically significant.
Different approaches can be used to decide on the sampling scheme that is to be used to get started. One could start with ∼10 sections and dimension the probes and the spacing between probes so that there will be ∼100 interactions between the probes and the feature of interest. The use of 10 sections has been shown to be an adequate starting point for Cavalieri estimates of the volumes of many biological structures (Gundersen and Jensen 1987). The rationale for starting with a minimum of 100 observations is provided in the section Why Sample 150 Positions? Because the group means will be unbiased, the worst that can happen using this relatively sparse sampling scheme is that you will need to sample twice the number of individuals than perhaps you would otherwise have to sample if you had sampled more of the individuals in the original group. On the other hand, you could start at the other extreme, be on the “safe side,” and use a sampling scheme that results in ∼1000 feature–probe interactions. At worst, this approach will require 10 times more work than is necessary and will significantly reduce the productivity of its followers. In this article, a pilot sampling scheme is described that has resulted in useful starting estimates in several studies of biological tissues. It must be emphasized that the suggested starting numbers are not sacrosanct. They represent a starting point that can be used to determine how much more or less sampling is needed to produce an optimal sampling scheme.
KNOW YOUR MATERIAL
The very first step in getting started with a stereological study of histological material is to become familiarized with the structure to be analyzed. Familiarity, in the context of a stereological study, means knowing where the features of interest are located within the structure that is being investigated.
In a laboratory that has routinely worked with serially sectioned material of entire structures of interest, the “usual” section intervals are most likely suitable in that the series will most likely contain more sections than necessary for a stereological analysis. It is unlikely that the sections in the series completely miss “important” features of the structure of interest in an individual. A Cavalieri estimate of the volume of the structure of interest in existing series and the subsequent calculation of the coefficients of error (CEs) of the estimates (see The Precision of Estimates in Stereological Analyses [West 2012b]) may serve to verify more rigorously the suitability of the series.
The situation may be different if one is unfamiliar with a structure or if previous analyses have focused on one or a few “representative” sections of a structure. In these cases, the first step toward establishing a suitable sectioning interval would be to consult an atlas. By flipping through the pages, one may quickly gain an impression of how much the structure varies in size from section to section and if there are sections in the series where the structure of interest is unusually large or small relative to the preceding or subsequent sections. From the coordinates provided in most atlases, a first qualified guess at a section interval that provides ∼10 sections that do not miss unusual peaks or troughs in the distribution may be obtained. Structures cut at this interval may then be subjected to the more rigorous analysis mentioned above.
Both of the above scenarios involve an analysis of the volume distribution of the structure of interest as a first step. Many regions of interest are defined by the fact that the cellular organization is similar throughout their extent and distinguish the region from its surroundings. In this case, number, length, or surface distributions can be expected to be similar to the volume distributions (Slomianka and West 2005) (see the section Plot the Distribution of the Features). If this is not the case; that is, if the features of interest are concentrated in parts of the region of interest, the distribution of the features needs to be considered before defining a sampling scheme.
The amount of effort invested into the development of a sampling scheme depends on the extent to which you expect design-based stereological procedures to become a part of laboratory routines. Ideally, you would embed one or two examples of the structure, section them exhaustively (or at least collect significantly more sections than you would expect to need), and analyze them by using increasingly smaller subsamples (see the sections Plot the Distribution of the Features and The Spacing Between Sections: Capturing the Peaks). In this way, you could empirically predict the CEs that are expected from a particular sampling scheme (Gundersen and Jensen 1987; Slomianka and West 2005). Although this approach is rather laborious, the resulting robust estimates of the CEs and their value in determining the appropriate amount of sampling (Plot the Distribution of the Features) will most likely offset the initial investment of additional time.
TISSUE PREPARATION
Regardless of how well one may be informed regarding the sampling and probing of a structure of interest, the quality of the numbers that are generated by design-based stereological procedures will not be better than the quality of the material that is being analyzed. Section series need not be perfect, but they should be near perfect. Data from a single section that has been lost from a random position in the series, during the processing of the tissue, may be replaced by interpolating data from adjacent sections in the series or from data from corresponding sections of adjacent series. There cannot be a systematic relationship between the sections that are lost and the experimental condition of the individual from which the sections are generated. Correction procedures have been implemented in the most widely used stereology software packages. However, any attempt to correct for imperfect material has the potential to generate errors in the final estimate and compromise the unbiasedness of estimates.
Material suitable for design-based stereological analysis can be prepared using all known histological techniques. Quality is more closely related to both experience and discipline than to any particular technique. This said, preparing either cryostat or paraffin sections seems to require more of both than the preparation of frozen or plastic sections. An example of a near perfect section series is illustrated in Figure 1. Notably, the sections were obtained from mouse brains. Antigen retrieval was performed by heating the section for an extended period of time, and staining was performed on free-floating sections. Before mounting, the sections looked like small cauliflowers. Although this may evoke understandable sighs and groans, it was not an impediment to ultimately producing a perfectly mounted series. In view of the plethora of histological methods that exist, it is beyond the scope of this article to describe how near perfect material can be generated for all types of material. It can be strongly recommended, however, that if problems arise, you seek the help of an experienced person.
Two immunocytochemically stained series (left, proliferation marker Ki67; right, microtubule associated protein doublecortin) of mouse brain sections containing hippocampus. Sagittal sections were cut frozen at 40 μm, subjected to antigen retrieval, and stained free-floating. No sections or parts of sections were lost from either series. Note that the top-right section of both series looks incomplete. They are the last sections cut from the hemispheres, in which parts of other structures already had disappeared. Sections of this type also need to be collected if they contain part of the region of interest. (Courtesy of Lutz Slomianka.)
Section Thickness
The thickness of the sections is a critical issue when getting started. In general, when you intend to use virtual three-dimensional (3D) probes, such as optical disectors and spaceballs, you should use the thickest possible sections in which you can observe the features of interest throughout the entire thickness. This is to ensure that the sections are thick enough to place an optical disector or spaceball probe between the upper and lower surfaces. One can determine whether or not the features of interest are stained throughout the depth of the section thickness by sampling several positions, within the region of interest, in a few sections and plotting the distribution of the feature on the axis along which one moves the focal plane. As a general rule, the thickness of the sections should be at least 20 μm after mounting, if you intend to use virtual 3D probes. This thickness will facilitate placement of the probes and the optimization of the dimensions of the probes. When volumes are estimated by point counting or object volumes are estimated with nucleator or rotator probes on vertical sections, the sections, be they physical or optical, should be as thin as possible to avoid overprojection.
PLOT THE DISTRIBUTION OF THE FEATURES
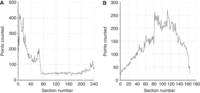
After deciding on an optimal section thickness, the distribution of the features of interest in one set of sections should be plotted (Fig. 2) as a function of the position of the section in the series. In most brain structures and other tissues, the amount of a particular feature on a section will be roughly proportional to the area of the structure on the section. This is because in most structures there is a fair degree of homogeneity in the features from section to section; that is, the density is relatively constant. For example, when observing the areas of the CA1 pyramidal cell layer along the sectioning axis, the number of neurons per unit volume NV of the layer changes little, but the area of the sections containing the neurons changes significantly (West and Gundersen 1990; Slomianka and West 2005). It is the volume of the structure at different positions, reflected in the sectional area of the sections series, which in most cases reflects the distribution of the features of interest along the sectioning axis. It is therefore possible, in most cases, to simply measure the areas of the region of interest on these sections by point counting and plot the number of points counted as a function of the position of the section in the series (Fig. 2). In cases in which the borders of the region that contains the structural features of interest are not readily defined (such as the raphe neurons of the brain stem and the neurons of nucleus basalis), it will be necessary to make fractionator estimates of these features of interest (numbers) on individual sections to get a feeling for the distribution of the feature of interest.
Points counted in the rat CA1 pyramidal cell layer in individual sections along the (A) dorsoventral axis (horizontal series) and (B) anteroposterior axis (coronal series) of the hippocampus reflecting the volume distribution of the CA1 pyramidal cell layer (Slomianka and West 2005). (Redrawn from Slomianka and West 2005.)
THE SPACING BETWEEN SECTIONS: CAPTURING THE PEAKS
The main objective of plotting the distribution of the structural features along the sectioning axis is to obtain information that can be used to determine the spacing between the sections that will be used to make the stereological estimate. This process will in effect define the number of sections to be used in any one individual. In structures with complicated 3D forms, there can be a small number of sections that contain a disproportionately large amount of the structure of interest. For example, the hippocampal pyramidal cell layer of CA1, in most species, is a laminar structure that is twisted in three dimensions. Depending on the angle at which the structure is sectioned, some of the sections can lie in the plane of the layer. In these, the layer will appear as a large area instead of a thin band of cells. These sections will appear as peaks in the plots of the distribution of section areas. When you decide on the intersectional distance to be used in the study, these peaks should be represented in the section series. That is, you would like to have an intersectional distance that is less than half of the width of the peaks. In Figure 2, the interval between sections to be sampled is dimensioned so that peaks, such as those seen within the first 20 sections and between sections 50–70 of the horizontally cut brain, will always be sampled. Accordingly, a section sample interval of 10 would be a good starting point. A similar section interval would be appropriate for the same region cut in the frontal plane, in view of the 20-sections-wide peak seen between the 80th and 100th sections. In the case of the horizontally sectioned hippocampus, a 10-section sampling interval would result in the use of ∼25 sections. This is most likely the upper limit with regard to the number of sections required for any analysis, in that few other structures in the brain have such complicated forms as the CA1 pyramidal cell layer.
Recall here that regardless of whether or not a systematic random sample of sections captures the peaks, the estimate of the total amount of the parameter (e.g., cell number, length, surface, volume) will be unbiased. As pointed out in the beginning of Systematic versus Random Sampling in Stereological Studies (West 2012c), one randomly placed section can be used to make an unbiased estimate. The issue here is the variance of the estimator. If a sampling interval is chosen that misses the peaks in the series obtained from some individuals, the estimate will be relatively low in these individuals. However, if a random starting point within the first sampling interval is chosen, the peaks will be represented in at least some series and produce relatively high estimates for these individuals. The mean across all individuals analyzed will approach the true mean with an increase in the number of individuals, that is, with an increase in n. Having very low and very high estimates in our sample does, however, increase the group variance and therefore decrease the chances of being able to detect possible group differences statistically. It is therefore desirable, at least at the start, to capture peaks that are deemed to contain a significant amount of information in the series. Capturing the “peaks” will reduce the VARSRS (see The Precision of Estimates in Stereological Analyses [West 2012b]) of the estimator and ultimately the number of individuals required in a study.
Capturing the peaks is not only important with regard to reducing the variance of an estimator, but also with regard to the conditions required for application of the quadratic approximation formula. That is, the intersectional data used to calculate the VARSRS (see The Precision of Estimates in Stereological Analyses [West 2012b]) are assumed to be from a continuous distribution. This is less so when peaks are missing, with the consequence that the distribution will be thought to be smoother than it actually is and the VARSRS will be underestimated.
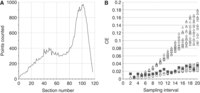
In a study that evaluated the effects of varying amounts of sampling on the precision of estimates of the number of cells in the rat hippocampal CA1 pyramidal cell layer, which has sharp peaks in its distribution when cut in the horizontal plane (Fig. 2A), the optimal sampling scheme used 20 sections to capture the “peaks” and reduce the VARSRS (Slomianka and West 2005). If there are no sharp peaks in the distribution—that is, there is a relatively smooth distribution of the structural features along the sectioning axis—the selection of far fewer than 20 systematic random sections will provide an adequate amount of precision for most estimators. For example, the volume distribution of the entire dentate gyrus in coronal sections contains only one broad peak (Fig. 3A). The CE (see The Precision of Estimates in Stereological Analyses [West 2012b]) remains below 4% even when every 20th section is sampled (Fig. 3B). Because the structure is represented in ∼120, 20-μm-thick sections, the selection of six or more sections would be sufficient to obtain estimator variances at or below 5% for estimates of volume.
(A) Volume distribution of the mouse dentate gyrus in coronal sections. (B) Estimates of the CE for different sampling intervals. For this structure, CE estimates that approach the empirically estimated CEs (squares, ▪) are obtained using m = 1 for smooth distributions (open circles, ○), whereas CE estimates using m = 0 for irregular distributions (triangles, ▵) overestimate estimator variance (for details regarding m, see The Precision of Estimates in Stereological Analyses [West 2012b]). Notably, for structures that show this type of quantitative behavior, estimator variance will be very small, even if only a few sections are analyzed. Using every 20th of the ∼120 sections available—that is, only five or six sections—will return estimates of the volume of this structure with a CE of <4%. (Courtesy of Lutz Slomianka.)
SPACING THE PROBES
After deciding on the embedding media, the type of stain, the section thickness, and the section interval, one can begin to
get a feeling for the spatial separation of the probes that are to be placed in or on the sections to be sampled. The first
step in this process is to sum the areas A of the region of interest on all the sections (n) to be analyzed, ΣA = A1 + A2 + · · · + An. This is the area on all of the sections that can potentially be hit with the probes. Next, the sum of the area is divided
by the number of probes that one wishes to place in this area. A good starting point for the number of probes is 150. Dividing
the available area by 150 will provide an approximation of the area associated with the movement from one sampling position
to the next sampling point on the sections, that is, ASTEP:
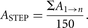(1)
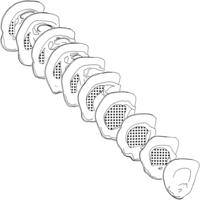
The square root of ASTEP associated with each probe location will be the x- and y-step sizes used in the analysis. Note that the number of probes placed on a particular section, if we use the same x- and y-step sizes on all sections, will be proportional to the area of the structure of interest on that section; that is, different numbers of probes will be placed in sections of different areas. This is as it should be, in that all parts of the region of interest must have equal probabilities of being sampled in order for the estimator to be unbiased (see, however, proportionator sampling, Box 1). The sections with the larger areas should be sampled proportionately more. This will not be the case if one performs the same amount of sampling on all sections, regardless of size (see Fig. 4).
The distance between the probes to be used in a pilot study (dots) can be determined by taking the sum of the areas of the sectional profiles of the region of interest (in this example, nine sections from the striatum of a rat brain) and dividing this by 150. Note that the number of probes in a section is proportionate to the area of the structure of interest in that section. (Redrawn from West et al. 1996.)
PROPORTIONATOR SAMPLING
This strategy outlined in The Spacing Between Sections: Capturing the Peaks and Spacing the Probes applies to uniform random sampling, which is the most widely applicable approach to sampling. There is an alternative approach, proportionator sampling, which may be more efficient for distributions that are nonuniform (Dorph-Petersen et al. 2000; Gardi et al. 2008). Certain features might be clustered, for example, specific cell types in the striatum. In these cases, one would perform more sampling in the regions where the features of interest are concentrated. That is, one would sample in proportion to the distribution of features of interest. The proportionator is essentially a two-pass approach and is well suited for automated analysis. One would first make a trial run to get a feeling for the distribution and then return and sample in more detail in proportion to the distribution observed after the first pass. This is a relatively new sampling strategy for stereological analyses with few examples to date in the central nervous system. An analog to this approach, applied to the sampling of sections, would be to use more sections in the regions of the peaks of the distributions and fewer sections in the regions where there is little change from section to section. For example, in Figure 2A, one would sample sections with a smaller intersectional spacing in the beginning of the series (left) as opposed to the later sections in the series (right), where little change occurs in the areas of the sectional profiles of the region of interest. The calculations of the efficiency of estimates made with proportional sampling are not the same as those described for uniform sampling (see Gardi et al. 2008).
If you do not have precise stepping motors and wish to make an estimate of a total quantity using the XTOTAL = XV × VREF approach, the ASTEP calculated above can be used to determine the amount of probes to be used on each section. That is, divide the area of the
region of interest on each section Asection by ASTEP to determine the number of independent randomly placed probes ηPROBES that should be made on that section to ensure that all parts of the region of interest have the same probability of being
sampled:
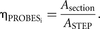(2)
Why Sample 150 Positions?
The rationale for dividing the sum of the area by 150 to obtain the ASTEP for the pilot study is based on the following considerations: If one thinks of the sample in an individual as an independent random sample, the CE of an estimate of this feature will be inversely proportional to the square root of the number of interactions (hits or counts) observed when the entire series is analyzed (see Systematic versus Random Sampling in Stereological Studies [West 2012c]). That is, when using independent random sampling, probes that return approximately one count per probe, the CE of the estimate can be expected, at best, to be ∼0.10 when 100 observations (counts) are made (see Box 2).
POISSON DISTRIBUTION
If the observations stem from a Poisson distribution (and there is some evidence that this is the case; L. Slomianka, pers.
comm.), when one uses a probe that on average returns one hit per probe, the SD (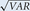
) of the mean of repeated estimates will be equal to the mean, and with 100 observations (n = 100), CE will have a value of 0.10 as shown in Equation 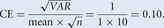3:
(3)
This sampling scheme is, strictly speaking, not an independent random sampling scheme, however, in that it also includes the systematic random sampling of sections and can be expected to be slightly different from this predicted result. Nonetheless, this is one way to get an idea regarding the spacing of the probes that can be used to get started. In the majority of stereological studies performed to date, this level of precision has proven to be a satisfactory starting point. After the first pilot data are collected, evaluations of the sampling scheme—taking into account the variation between sections, VARSRS, and within sections, S2—can then be used to tweak the sampling scheme.
Why, then, use 150 instead of 100 sampling locations? First, although the statistical average for the average number of hits in the series of sections would be 100 if we calculated ASTEP for 100 hits, the random systematic placement of samples will result in slightly fewer or more hits if we analyzed the series several times. Selecting a slightly larger number, it is likely that we will have a minimum of 100 sampling locations in the series. Second, the area of the sections to be sampled will also vary from one series of sections to the next within an individual, because of the random systematic selection of sections. Again, calculating ASTEP for a slightly larger number of hits will ensure a sufficient number of sampling locations in each series of an individual. Third, the individuals in our sample may differ. A sampling scheme developed for the “average” individual (if, indeed, you were lucky enough to select that particular one when developing the sampling scheme) may not return the number of samples desired in “small” individuals that may be in the group. Finally, the degree to which the distribution is actually a Poisson distribution is uncertain, and deviations most likely will result in larger CEs than predicted. By aiming for a slightly larger number of observations than 100 as a starting point, one can be relatively confident that the number of probe samples to be made will be more than adequate to obtain an appropriate CE. In the majority of stereological studies performed to date, 150 counts and 10 sections have proven to be a satisfactory starting point.
DIMENSIONING THE PROBE
Optimally, the probe itself should be dimensioned so that it will result, on average, in one interaction (“count,” “hit”) at each position probed. Optimally, one would aim for approximately one count or hit per position or ∼150 counts total for each individual estimate. If the counts are obtained while sitting in front of the microscope and observing the sections, disector probes that have a small frame area Aframe and a large disector height are typically easier to work with than probes that have a large Aframe and a small disector height.
It is possible to make an unbiased estimate from one randomly placed megaprobe that results in many hits or counts. From the standpoint of efficiency, that is, capturing any variability caused by an uneven distribution of the feature within the structure of interest, it is better to spread the 150 observations as much as possible throughout the region of interest, to reduce the variance of the estimator. This is accomplished by dimensioning the probe (volume of the optical disector, surface of the spaceball) so that each probe, on average, results in one interaction (i.e., count or hit) when positioned in the region of interest. The probe can initially be set to an arbitrary size that is comfortable to work with and eventually adjusted by trial and error, with reference to the pilot data, to give one hit per probe. If this results in too many or too few counts, reduce or increase, respectively, the size (area, volume, length) of the probes so that 150 probes will provide, on average, roughly 150 hits.
The expression “on average,” which here has been used when referring to the number of hits or interactions between probe and structural feature, has to be taken with some degree of caution in this particular context. It is possible that our sampling scheme returns 150 interactions from 150 probes, but all of the interactions may have been obtained with a few probes. This would suggest an uneven distribution of the feature in the sections. There is a risk that we would miss subregions in which most of the features are located if the sections were sampled again or if another section series from the same individual was sampled. To reduce this risk, that is, to reduce estimator variance, one can decrease ASTEP and the size of the probe to obtain more probes and more interactions. Unfortunately, this will also increase the number of “empty probes” (i.e., probes in which there are no interactions). However, in practice, it takes less time to analyze empty probes. They are not a major burden and, if there are a sufficient number of probes with interactions, they actually slightly improve estimator variance of NV or the density of any other parameter, in that they do contain information regarding the density of the feature at those sampling locations, namely, 0. However, if you feel that they represent an unacceptable amount of additional work, consider defining the structure of interest in a way that confines the areas probed to those areas in which the feature is actually present. Another reason for using probes that result in a small number of interactions per probe is that it has been empirically shown that they more closely fulfill the Poisson-criterion assumption that is involved in the calculation of the section noise S2 that contributes to the CE (see The Precision of Estimates in Stereological Analyses [West 2012b]).
CALCULATE THE PILOT OCE
After making an estimate of the structural parameter of interest in one individual with the pilot sampling scheme, you can make an estimate of the CE of the estimate as described in The Precision of Estimates in Stereological Analyses (West 2012b). If it is on the order of 0.10, a value shown to be appropriate for the majority of studies, make an estimate on at least one additional pilot individual, using the same sampling scheme, to ensure that the first individual was representative of the group. If the average of the OCEINDIVIDUAL is ∼0.10, move to the next stage of the pilot study.
STEREOLOGISTS DO IT BLIND
In comparative studies involving groups and individuals, it is important to conduct the studies blind. When collecting stereological data, one has to make decisions as to whether the probe is interacting with a structural feature. These decisions should be clear-cut in the vast majority of circumstances. There will, however, inevitably be a few occasions when that is not the case. It is best in these situations to be blind to the identity of the individual or group. This implies that the same sampling scheme should be used on all of the individuals in a study, even though the scheme may not be optimal for some of the individuals. There are several ways to accomplish this, although there are no hard and fast rules. One way is to be sure that the sampling scheme is optimal for the group with the lowest values. Another is to use a sampling scheme that lies between the optimal schemes for both groups. In practice, it is also helpful to pay no attention to the counts as they develop in an individual and across individuals as the study progresses—that is, the totals of the features that are being estimated are first calculated when all individuals are done.
This could be done by mixing the slides from different individuals when counting. There are studies in which groups are immediately recognizable because of differences in the appearance of the structure and/or features of interest, and in which it will become difficult to perform the study blind without creating other pitfalls.
GETTING STARTED WITH LOCAL ESTIMATORS
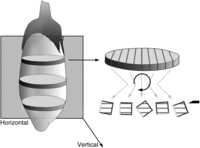
Many of the same considerations described above, for the sampling required for global estimators, apply to the initial steps to be taken when making estimates of the mean volume of individual objects with methods such as the nucleator and rotator. Again, the overriding consideration is to make sure that all of the objects in the region of interest have an equal probability of being sampled. In addition, it is important to ensure that the linear (nucleator) or areal (rotator) probe interacts isotropically with the objects in 3D space. This is most readily accomplished through the use of vertical sections. It is therefore important that the vertical sections be obtained from representative slabs from the region of interest. This is best achieved by taking vertical sections from systematic random samples of slabs cut along one axis of the structure of interest and keeping the number of nucleator or rotator probes proportional to the volume (area) of the slabs (Fig. 5). It is also important that the objects to be measured (e.g., cells, nuclei, mitochondria) be selected with disectors to ensure a number-weighted selection of objects.
After sectioning the structure into slabs, estimate the area of the region of interest in each slab on a section from the face of the slab. This is performed before the second sectioning, which results in vertical sections. The amount of sampling in the vertical sections that stems from a particular slab should be proportional to the area of the slab, before the generation of the vertical sections, that is, the second sectioning. (Courtesy of Lutz Slomianka.)
For local estimators, it is possible to use the same rationale for making 150 observations as the one used for the global
estimator. Determine the areas of the sections obtained from the slabs and divide the sum of these areas by 150. Next, randomly
distribute the sampling with the local estimator probe on the vertical sections in proportion to the area of the slabs from
which the vertical sections were made. In this case, the variance of the estimator can be made with standard statistics:
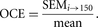(4)
The same strategy used for optimizing studies that involve global estimates can be used to optimize the sampling, at the level
of groups, when making local estimates, as described in The Precision of Estimates in Stereological Analyses (West 2012b):
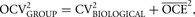(5)
where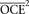 
is the mean of the squared CEs for individuals in the groups or the observed CE of the estimator.
It is also important to remember that n in any statistical comparison of data of this type is equal to the number of individuals in the study and not the number of objects counted or measured.
- © 2013 Cold Spring Harbor Laboratory Press
